By: Steve Bilow, Senior Product Marketing Manager
Let us continue our journey into Dynamic Range concepts that we began in our previous post by discussing how, throughout the video chain, we use the mathematical constructs called Transfer Functions to mimic the way our eyes see, and to adjust color and dynamic range accordingly.
Why do we need Transfer functions?
Our eyes do not perceive light as cameras do. A digital video camera will yield a linear output with respect to input light intensity. The magnitude of the output signal doubles when you double the number of photons that hit the sensor. In our first post, we explained how human vision differs. Recall, for example, that we have greater sensitivity to differences in dark versus light. Adapting a camera’s output, or the brightness of a display, to what we see requires a set of functions to change linear models into perceptually accurate ones.
Working Spaces
When changing the characteristics of a signal you must either do so with reference to the scene that is being captured or to the device you are using to view the image. The first is called “Scene Referred Space” and the second, “Display Referred Space”. Modifying an image in Display Referred Space limits your result to looking appropriate only on a specific display. That’s great if you are rendering a final production for a format like a 4K television, a DolbyVision theater projector, or a BluRay disc. That’s what you need to do. But when it comes to editing and color grading, staying in a Scene Referred space as long as possible gives you the most flexibility. When considering Transfer Functions, we will always work from one of these 2 reference points.

OETF (Optical Electrical Transfer Function): How cameras turn optical signals into voltages/bits
The camera-captured “linear” light is converted to an electrical signal using a non-linear function known as the Opto-Electrical Transfer Function (OETF). It involves a quantization process that restricts the electrical (digital) signal to a certain bit depth. OETF-based quantization is sometimes followed by compression for storage and/or transmission.
EOTF (Electrical Optical Transfer Function): How displays turn electrical signals into visual stimuli
For displays, an electrical signal must be converted back to an image. This is another non-linear function called the Electro-Optical Transfer Function (EOTF). The EOTF is not a simple inversion of the OETF. That would only work if the photons going into a camera lens and hitting a sensor, and those being displayed by a display device had identical characteristics. They do not. The input for an OETF is the light that is captured by a camera. The output of an EOTF needs to be the light that is displayed by a television, monitor, or projector. That is why these transfer functions are independent.
OOTF (Opto-Optical Transfer Function): Vision Science from OETF to EOTF
The whole video acquisition, processing, and display pipeline involves a third mathematical formulation called an Opto-Optical Transfer Function (OOTF). If you define any 2 of these functions, you can derive the third. Since we want to work in either Scene Referred or Display Referred space, let’s assume for this discussion that OETF and EOTF are the 2 known functions.

The Legacy: Gamma Curves are Transfer Functions
Like many things in the television business, we carry forward a legacy from the early days of broadcast TV. Traditionally, the EOTF used for CRT displays was called a “gamma” curve. CRTs have some distinct characteristics that result in a nonlinear relationship between applied voltage and beam intensity in an electron gun That nonlinearity is called “gamma”. We no longer must deal with this anomaly, but we are going to build the rest of our discussion on that foundation. After all, we may not have electron beams and phosphor to deal with, but almost all know the words “Gamma 2.4”. This EOTF is, even today, discussed in ITU-R BT.1886. The OETF used for capture in standard television is typically BT.709 and, that too should be amply familiar to most of us. These curves originally compensated for non-linearities in the electron beams in picture tube guns, but it is these concepts that carry us into HDR.

PQ and HLG: HDR Standard Transfer Functions
CRTs may be old technology but the concepts we just discussed are equally applicable to HD, 4K, and 8K displays. These concepts are needed with all modern technologies from LCD panels with LED backlights and Quantum Dot (Qdot) support, to OLED displays, LASER cinema projectors, and MicroLED displays. It matters not whether the display technology is old or new, additive or subtractive, projected or embedded in a panel. Transfer Functions matter. In fact, for HDR, you may see different curves, but we still need those curves.
That is why everyone from the BBC and NHK, to ARIB and SMPTE, to the vision scientists at Dolby, and every display and camera manufacturer is working to perfect them. Let us look at the major standards.
Hybrid-Log-Gamma
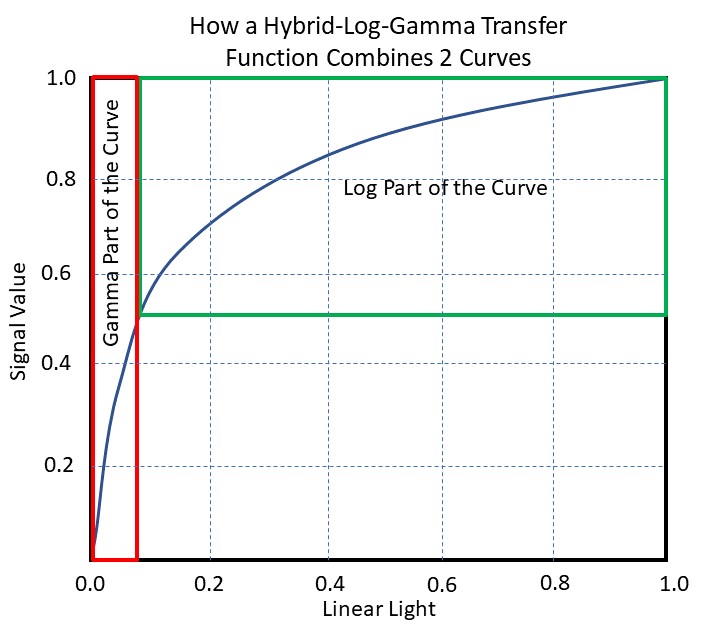
SDR and HDR display have clear differences, yet it is beneficial to be able to send a single bitstream to either. To make this happen, the BBC and NHK jointly proposed a new OETF called Hybrid-Log-Gamma (HLG). This is described in the Association of Radio Industries and Businesses (ARIB) standard STD-B67. This function is called Hybrid-Log-Gamma (HLG) for practical reasons. The lower half of the signal values use a gamma curve, and the upper half is logarithmic. This hybrid OETF allows a device to send a single bitstream that is compatible with both SDR and HDR displays.

Perceptual Quantization
To accommodate HDR, a new EOTF was derived to adapt more closely to human vision. This is called a “PQ” (Perceptual Quantization). It uses a just noticeable difference (JND) based on a visual contrast sensitivity function called Barten’s model. While explaining the model is far beyond the scope of a blog post, we need to, at least, tell you what the words mean before moving on. So, here goes.
Barten’s Model
Barten’s Model mathematically considers many aspects of human vision including neuron noise, lateral inhibition, photon noise, external noise, the brain’s limits on the integration we all tried to forget from Calculus 101, an optical modulation transfer function, spatial orientation, and temporal filtering. Here are a few simple details:
- Neuron noise expresses the upper limit of Contrast Sensitivity at high spatial frequencies. Low spatial frequencies seem like they are attenuated by lateral inhibition in ganglion cells.
- Photon noise represents changes in photon flux, pupil diameter, and the quantum detection efficiency of the eye.
- We could go on but won’t torture you more. Now you know why this is far beyond the scope of this post.
PQ uses this complex mathematical model to attain “perceptually uniform” signal quantization. Because it resembles the human perceptual model, it efficiently uses data through the complete luminance range. A PQ-encoded signal can represent luminance levels up to 10 000 nits with relative efficiency. This EOTF was standardized by SMPTE in 2014 as ST 2084.
To Mimic Human Perception Requires Transfer Functions
It should now be clear that these transfer functions essentially combine gamma, power functions, and log functions with some detailed perceptual models to mimic the non-linearity of the human visual system. Let’s sum it all up this way. A camera sensor may respond linearly to light. But, from that point on, almost everything else does not. From the relationship between voltage and electron output in a CRT picture tube, to the dynamic resolution of the human eye across light intensities, dynamic range (and to no lesser extent color) is nonlinear. As we have progressed through generations from those old CRT displays to Qdot backlit LCD panels and Laser/Phosphor digital cinema projectors, we still need transfer functions to ensure visual perceptual accuracy. Adjusting for those nonlinearities is why we need transfer functions now and into the future.